For $\lambda \in (0,\,1/2]$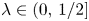 let $K_\lambda \subset \mathbb {R}$ 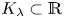be a self-similar set generated by the iterated function system $\{\lambda x,\, \lambda x+1-\lambda \}$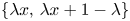. Given $x\in (0,\,1/2)$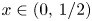, let $\Lambda (x)$ 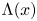be the set of $\lambda \in (0,\,1/2]$ 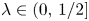such that $x\in K_\lambda$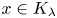. In this paper we show that $\Lambda (x)$ 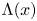is a topological Cantor set having zero Lebesgue measure and full Hausdorff dimension. Furthermore, we show that for any $y_1,\,\ldots,\, y_p\in (0,\,1/2)$ 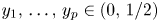there exists a full Hausdorff dimensional set of $\lambda \in (0,\,1/2]$ 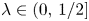such that $y_1,\,\ldots,\, y_p \in K_\lambda$.

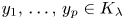The study is an experimental and theoretical analysis of the patterns of traffic flows and the possibilities of their distribution on urban street and road networks. It considers and analyses modern approaches that make it possible to improve traffic flow control mechanisms and traffic conditions on a street and road network. Based on the established internal relationships, the paper develops a model of the influence of factors on the level of their priority, which makes it possible to divide them by hierarchy levels and, accordingly, to observe the level of their impact on independent components. The scientific novelty of the research lies in the newly developed method of vehicle traffic control, which involves the distribution of traffic flows along the urban street and road network. The conclusions presented in the study represent scientific and methodological developments and applied recommendations that can be used in urban planning to improve the conditions of transport services in populated areas.

Let $\mathcal{F}$ be an intersecting family. A $(k-1)$-set $E$ is called a unique shadow if it is contained in exactly one member of $\mathcal{F}$. Let ${\mathcal{A}}=\{A\in \binom{[n]}{k}\colon |A\cap \{1,2,3\}|\geq 2\}$. In the present paper, we show that for $n\geq 28k$, $\mathcal{A}$ is the unique family attaining the maximum size among all intersecting families without unique shadow. Several other results of a similar flavour are established as well.

Because mechanical operations are performed only up to a certain precision, the geometry of parts involved in real-life products is never known precisely. But if tolerance models for specifying acceptable variations have received a substantial attention, operations on toleranced objects have not been studied extensively. That is the reason why we address in this paper the computation of the union and the intersection of toleranced simple polygons, under a simple and already known tolerance model. First, we provide a practical and efficient algorithm that stores in an implicit data structure the information necessary to answer a request for specific values of the tolerances without performing a computation from scratch. If the polygons are of sizes m and n, and s is the number of intersections between edges occurring for all the combinations of tolerance values, the preprocessed data structure takes O(s) space and the algorithm that computes a union/intersection from it takes O((n + m)log s + k' + k log k) time, where k is the number of vertices of the union/intersection and k ≤ k' ≤ s. Although the algorithm is not output sensitive, we show that the expectations of k and k' remain within a constant factor τ, a function of the input geometry. Second, we define and study the stability of union or intersection features. Third, we list interesting applications of the algorithms related to feasibility of assembly and assembly sequencing of real assemblies.

In this paper, we prove two versions of an arithmetic analogue of Bezout's theorem, subject to some technical restrictions. The basic formula proven is deg(V)h(X∩Y)=h(X)deg(Y)+h(Y)deg(X)+O(1), where X and Y are algebraic cycles varying in properly intersecting families on a regular subvariety VS⊂PSN. The theorem is inspired by the arithmetic Bezout inequality of Bost, Gillet, and Soulé, but improve upon it in two ways. First, we obtain an equality up to O(1) as the intersecting cycles vary in projective families. Second, we generalise this result to intersections of divisors on any regular projective arithmetic variety.

Let f:X→S be a projective morphism of Noetherian schemes. We assume f purely of relative dimension d and finite Tor-dimensional. We associate to d+1 invertible sheaves $\cal L$1,$\ldots$,$\cal L$d+1 on X a line bundle IX/S($\cal L$1,$\ldots$,$\Cal L$d+1) on S depending additively on the $\cal L$i, commuting to ‘good’ base changes and which represents the integral along the fibres of f of the product of the first Chern classes of the $\cal L$i. If d=0, IX/S($\cal L$) is the norm $\cal N$X/S($\cal L$).