1 results
A fixed-point curve theorem for finite-orbits local diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 16 February 2023, pp. 4138-4165
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
-
We study local biholomorphisms with finite orbits in some neighborhood of the origin since they are intimately related to holomorphic foliations with closed leaves. We describe the structure of the set of periodic points in dimension 2. As a consequence we show that given a finite-orbits local biholomorphism F, in dimension 2, there exists an analytic curve passing through the origin and contained in the fixed-point set of some non-trivial iterate of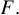
$F.$ As an application we obtain that at least one eigenvalue of the linear part of F at the origin is a root of unity. Moreover, we show that such a result is sharp by exhibiting examples of finite-orbits local biholomorphisms such that exactly one of the eigenvalues is a root of unity. These examples are subtle since we show they cannot be embedded in one-parameter groups.
