1 results
Scaling laws for non-Euclidean plates and theW2,2 isometric immersions of Riemannian metrics
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 4 / October 2011
- Published online by Cambridge University Press:
- 28 October 2010, pp. 1158-1173
- Print publication:
- October 2011
-
- Article
- Export citation
-
Recall that a smooth Riemannian metric on a simply connected domain canbe realized as the pull-back metric of an orientation preserving deformation ifand only if the associated Riemann curvature tensor vanishes identically.When this condition fails, one seeks a deformation yielding the closest metric realization. We set up a variational formulation of this problem byintroducing the non-Euclidean version of the nonlinear elasticity functional, and establish its Γ-convergence under the properscaling. As a corollary, we obtain new necessary and sufficient conditions for existence of a W2,2 isometric immersion of a given 2d metricinto $\mathbb R^3$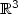
.
