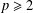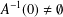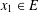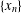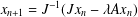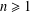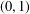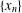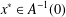Refine search
Actions for selected content:
5 results
COMPUTATION OF ZEROS OF MONOTONE TYPE MAPPINGS: ON CHIDUME’S OPEN PROBLEM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 05 February 2020, pp. 278-288
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Exact simulation of multidimensional reflected Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 137-156
- Print publication:
- March 2018
-
- Article
- Export citation
Stability Analysis on the Algorithm of Constitutive Relation in Viscoplastic Materials
-
- Journal:
- Journal of Mechanics / Volume 33 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 03 June 2016, pp. 173-181
- Print publication:
- April 2017
-
- Article
- Export citation
The Practical Replacement of a Bonus-Malus System
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 31 / Issue 2 / November 2001
- Published online by Cambridge University Press:
- 29 August 2014, pp. 317-335
- Print publication:
- November 2001
-
- Article
-
- You have access
- Export citation