We deal with the filtering problem of a general jump diffusion process, X, when the observation process, Y, is a correlated jump diffusion process having common jump times with X. In this setting, at any time t the σ-algebra 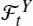 provides all the available information about Xt, and the central goal is to characterize the filter, πt, which is the conditional distribution of Xt given observations
provides all the available information about Xt, and the central goal is to characterize the filter, πt, which is the conditional distribution of Xt given observations 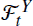 . To this end, we prove that πt solves the Kushner-Stratonovich equation and, by applying the filtered martingale problem approach (see Kurtz and Ocone (1988)), that it is the unique weak solution to this equation. Under an additional hypothesis, we also provide a pathwise uniqueness result.
. To this end, we prove that πt solves the Kushner-Stratonovich equation and, by applying the filtered martingale problem approach (see Kurtz and Ocone (1988)), that it is the unique weak solution to this equation. Under an additional hypothesis, we also provide a pathwise uniqueness result.