Given a group automorphism 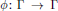 $\phi :\,\Gamma \,\to \,\Gamma $, one has an action of
$\phi :\,\Gamma \,\to \,\Gamma $, one has an action of  $\Gamma $ on itself by
$\Gamma $ on itself by 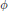 $\phi $-twisted conjugacy, namely,
$\phi $-twisted conjugacy, namely, 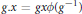 $g.x\,=\,gx\phi ({{g}^{-1}})$. The orbits of this action are called
$g.x\,=\,gx\phi ({{g}^{-1}})$. The orbits of this action are called 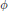 $\phi $-twisted conjugacy classes. One says that
$\phi $-twisted conjugacy classes. One says that  $\Gamma $ has the
$\Gamma $ has the 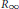 ${{R}_{\infty }}$-property if there are infinitely many
${{R}_{\infty }}$-property if there are infinitely many 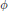 $\phi $-twisted conjugacy classes for every automorphism
$\phi $-twisted conjugacy classes for every automorphism 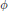 $\phi $ of
$\phi $ of  $\Gamma $. In this paper we show that
$\Gamma $. In this paper we show that 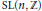 $\text{SL(}n\text{,}\mathbb{Z}\text{)}$ and its congruence subgroups have the
$\text{SL(}n\text{,}\mathbb{Z}\text{)}$ and its congruence subgroups have the 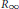 ${{R}_{\infty }}$-property. Further we show that any (countable) abelian extension of
${{R}_{\infty }}$-property. Further we show that any (countable) abelian extension of  $\Gamma $ has the
$\Gamma $ has the 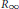 ${{R}_{\infty }}$-property where
${{R}_{\infty }}$-property where  $\Gamma $ is a torsion free non-elementary hyperbolic group, or
$\Gamma $ is a torsion free non-elementary hyperbolic group, or 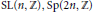 $\text{SL(}n\text{,}\mathbb{Z}\text{)},\text{Sp(2}n\text{,}\mathbb{Z}\text{)}$ or a principal congruence subgroup of
$\text{SL(}n\text{,}\mathbb{Z}\text{)},\text{Sp(2}n\text{,}\mathbb{Z}\text{)}$ or a principal congruence subgroup of 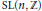 $\text{SL(}n\text{,}\mathbb{Z}\text{)}$ or the fundamental group of a complete Riemannian manifold of constant negative curvature.
$\text{SL(}n\text{,}\mathbb{Z}\text{)}$ or the fundamental group of a complete Riemannian manifold of constant negative curvature.
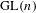 $\text{GL}(n)$ AND
$\text{GL}(n)$ AND 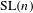 $\text{SL}(n)$
$\text{SL}(n)$