In practice, it is common that a best fitting structural equation model (SEM) is selected from a set of candidate SEMs and inference is conducted conditional on the selected model. Such post-selection inference ignores the model selection uncertainty and yields too optimistic inference. Using the largest candidate model avoids model selection uncertainty but introduces a large variation. Jin and Ankargren (Psychometrika 84:84–104, 2019) proposed to use frequentist model averaging in SEM with continuous data as a compromise between model selection and the full model. They assumed that the true values of the parameters depend on \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$n^{-1/2}$$\end{document}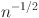 with n being the sample size, which is known as a local asymptotic framework. This paper shows that their results are not directly applicable to SEM with ordinal data. To address this issue, we prove consistency and asymptotic normality of the polychoric correlation estimators under the local asymptotic framework. Then, we propose a new frequentist model averaging estimator and a valid confidence interval that are suitable for ordinal data. Goodness-of-fit test statistics for the model averaging estimator are also derived.
with n being the sample size, which is known as a local asymptotic framework. This paper shows that their results are not directly applicable to SEM with ordinal data. To address this issue, we prove consistency and asymptotic normality of the polychoric correlation estimators under the local asymptotic framework. Then, we propose a new frequentist model averaging estimator and a valid confidence interval that are suitable for ordinal data. Goodness-of-fit test statistics for the model averaging estimator are also derived.