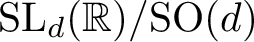 $\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$ IN THE BENJAMINI–SCHRAMM LIMIT
$\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$ IN THE BENJAMINI–SCHRAMM LIMIT
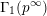 $\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations
$\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations
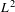 $L^{2}$-ANALYTIC TORSION FOR ARITHMETIC QUOTIENTS OF THE SYMMETRIC SPACE
$L^{2}$-ANALYTIC TORSION FOR ARITHMETIC QUOTIENTS OF THE SYMMETRIC SPACE 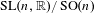 $\operatorname{SL}(n,\mathbb{R})/\operatorname{SO}(n)$
$\operatorname{SL}(n,\mathbb{R})/\operatorname{SO}(n)$