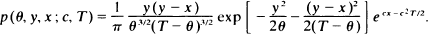We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We give a simple expression for the joint probability density of: (a) the maximum value Y = max [X(t), 0 ≦ t ≦ T); (b) its location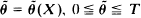 
; (c) the endpoint X(T), where X(t) = Xc(t) is a Wiener process with drift, Xc(t) = W(t) + ct, 0 ≦ t ≦ T. That is, we find the density p(θ, y, x) = p(θ, y, x; c, T) of 
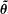, Y, X(T), p(θ, y, x; 
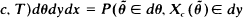, Xc(T) ∈ dx) is given by, 0 < θ < T, x ≦ y, 0 < y,
