We show that any Kawamata log terminal del Pezzo surface over an algebraically closed field of large characteristic is globally 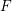 $F$-regular or it admits a log resolution which lifts to characteristic zero. As a consequence, we prove the Kawamata–Viehweg vanishing theorem for klt del Pezzo surfaces of large characteristic.
$F$-regular or it admits a log resolution which lifts to characteristic zero. As a consequence, we prove the Kawamata–Viehweg vanishing theorem for klt del Pezzo surfaces of large characteristic.