We study stationary solutions to the Keller–Segel equation on curved planes. We prove the necessity of the mass being $8 \pi$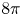 and a sharp decay bound. Notably, our results do not require the solutions to have a finite second moment, and thus are novel already in the flat case. Furthermore, we provide a correspondence between stationary solutions to the static Keller–Segel equation on curved planes and positively curved Riemannian metrics on the sphere. We use this duality to show the nonexistence of solutions in certain situations. In particular, we show the existence of metrics, arbitrarily close to the flat one on the plane, that do not support stationary solutions to the static Keller–Segel equation (with any mass). Finally, as a complementary result, we prove a curved version of the logarithmic Hardy–Littlewood–Sobolev inequality and use it to show that the Keller–Segel free energy is bounded from below exactly when the mass is $8 \pi$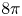, even in the curved case.

We introduce a multi-species chemotaxis type system admitting an arbitrarily large number of population species, all of which are attracted versus repelled by a single chemical substance. The production versus destruction rates of the chemotactic substance by the species is described by a probability measure. For such a model, we investigate the variational structures, in particular, we prove the existence of Lyapunov functionals, we establish duality properties as well as a logarithmic Hardy–Littlewood–Sobolev type inequality for the associated free energy. The latter inequality provides the optimal critical value for the conserved total population mass.