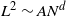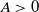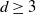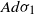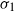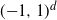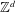Refine search
Actions for selected content:
3 results
4 - Statistical Physics on Random Planar Maps
-
- Book:
- Gaussian Free Field and Liouville Quantum Gravity
- Published online:
- 20 November 2025
- Print publication:
- 04 December 2025, pp 133-167
-
- Chapter
- Export citation
Interlacement limit of a stopped random walk trace on a torus
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 354-388
- Print publication:
- March 2024
-
- Article
- Export citation
Geometry of Uniform Spanning Forest Components in High Dimensions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1297-1321
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation