1 results
On the loss of compactness in the vectorial heteroclinic connection problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 22 March 2016, pp. 595-608
- Print publication:
- June 2016
-
- Article
- Export citation
-
We give an alternative proof of the theorem of Alikakos and Fusco concerning existence of heteroclinic solutions U : ℝ → ℝN to the system
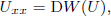
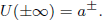
Here a± are local minima of a potential W ∈ C2(ℝN) with W(a±) = 0. This system arises in the theory of phase transitions. Our method is variational but differs from the original artificial constraint method of Alikakos and Fusco and establishes existence by analysing the loss of compactness in minimizing sequences of the action in the appropriate functional space. Our assumptions are slightly different from those considered previously and also imply a priori estimates for the solution.
