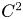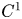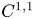We compare two standard approaches to defining lower Ricci curvature bounds for Riemannian metrics of regularity below $C^2$. These are, on the one hand, the synthetic definition via weak displacement convexity of entropy functionals in the framework of optimal transport, and the distributional one based on non-negativity of the Ricci-tensor in the sense of Schwartz. It turns out that distributional bounds imply entropy bounds for metrics of class $C^1$ and that the converse holds for $C^{1,1}$-metrics under an additional convergence condition on regularizations of the metric.

In this paper, we revisit a priori error analysis of nonconforming finite element methods for the Poisson problem. Based on some techniques developed in the context of the a posteriori error analysis, under two reasonable assumptions on the nonconforming finite element spaces, we prove that, up to some oscillation terms, the consistency error can be bounded by the approximation error. We check these two assumptions for the most used lower order nonconforming finite element methods. Compared with the classical error analysis of the nonconforming finite element method, the a priori analysis herein only needs the H1 regularity of the exact solution.