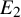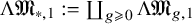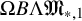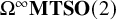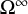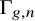Refine search
Actions for selected content:
4 results
Parametrised moduli spaces of surfaces as infinite loop spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HOLOMORPHIC FLEXIBILITY PROPERTIES OF SPACES OF ELLIPTIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 02 March 2017, p. 515
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
FUNCTORIAL ASPECTS OF THE RECONSTRUCTION OF LIE GROUPOIDS FROM THEIR BISECTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 14 March 2016, pp. 253-276
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
On Steenrod Bundles and the van Kampen Theorem
-
- Journal:
- Canadian Mathematical Bulletin / Volume 31 / Issue 2 / 01 June 1988
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-249
- Print publication:
- 01 June 1988
-
- Article
-
- You have access
- Export citation