1 results
Series which are both max-plus and min-plus rational are unambiguous
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 40 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 15 October 2005, pp. 1-14
- Print publication:
- January 2006
-
- Article
- Export citation
-
Consider partial maps ∑* → $\mathbb R$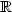
with a rational
domain. We show that two families of such series are actually the
same: the unambiguous rational series on the one hand, and
the max-plus and min-plus rational series on the other hand.
The decidability of equality was known to hold in both families with
different proofs, so the above unifies the picture.
We give an effective procedure to build an unambiguous automaton from
a max-plus automaton and a min-plus one that recognize the same series.
