We study Serre duality in the singularity category of an isolated Gorenstein singularity and find an explicit formula for the duality pairing in terms of generalised fractions and residues. For hypersurfaces we recover the residue formula of the string theorists Kapustin and Li. These results are obtained from an explicit construction of complete injective resolutions of maximal Cohen–Macaulay modules.

In a recent paper, Iyama and Yoshino considered two interesting examples of isolated singularities over which it is possible to classify the indecomposable maximal Cohen–Macaulay modules in terms of linear algebra data. In this paper, we present two new approaches to these examples. In the first approach we give a relation with cluster categories. In the second approach we use Orlov’s result on the graded singularity category.

For a commutative local ring 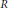$R$, consider (noncommutative) 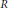$R$-algebras $\Lambda$ of the form 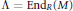$\Lambda \,=\,\text{En}{{\text{d}}_{R}}\left( M \right)$ where 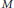$M$ is a reflexive 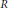$R$-module with nonzero free direct summand. Such algebras $\Lambda$ of finite global dimension can be viewed as potential substitutes for, or analogues of, a resolution of singularities of Spec 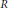$R$. For example, Van den Bergh has shown that a three-dimensional Gorenstein normal $\mathbb{C}$-algebra with isolated terminal singularities has a crepant resolution of singularities if and only if it has such an algebra $\Lambda$ with finite global dimension and which is maximal Cohen-Macaulay over 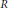$R$ (a “noncommutative crepant resolution of singularities”). We produce algebras 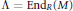$\Lambda \,=\,\text{En}{{\text{d}}_{R}}\left( M \right) $ having finite global dimension in two contexts: when 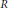$R$ is a reduced one-dimensional complete local ring, or when 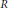$R$ is a Cohen-Macaulay local ring of finite Cohen–Macaulay type. If in the latter case 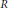$R$ is Gorenstein, then the construction gives a noncommutative crepant resolution of singularities in the sense of Van den Bergh.