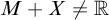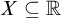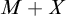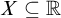By the Galvin–Mycielski–Solovay theorem, a subset X of the line has Borel’s strong measure zero if and only if 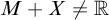$M+X\neq \mathbb {R}$ for each meager set M.

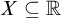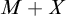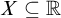A set $X\subseteq \mathbb {R}$ is meager-additive if $M+X$ is meager for each meager set M. Recently a theorem on meager-additive sets that perfectly parallels the Galvin–Mycielski–Solovay theorem was proven: A set $X\subseteq \mathbb {R}$ is meager-additive if and only if it has sharp measure zero, a notion akin to strong measure zero.

We investigate the validity of this result in Polish groups. We prove, e.g., that a set in a locally compact Polish group admitting an invariant metric is meager-additive if and only if it has sharp measure zero. We derive some consequences and calculate some cardinal invariants.