We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The asymptotic mean value Laplacian—AMV Laplacian—extends the Laplace operator from $\mathbb {R}^n$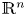
to metric measure spaces through limits of averaging integrals. The AMV Laplacian is however not a symmetric operator in general. Therefore, we consider a symmetric version of the AMV Laplacian, and focus lies on when the symmetric and non-symmetric AMV Laplacians coincide. Besides Riemannian and 3D contact sub-Riemannian manifolds, we show that they are identical on a large class of metric measure spaces, including locally Ahlfors regular spaces with suitably vanishing distortion. In addition, we study the context of weighted domains of $\mathbb {R}^n$
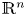—where the two operators typically differ—and provide explicit formulae for these operators, including points where the weight vanishes.
