In many sports contests, the equilibrium requires players to randomize across repeated rounds, i.e., exhibit no temporal predictability. Such sports data present a window into the (in)efficiency of random sequence generation in a natural competitive environment, where the decision makers (tennis players) are both highly experienced and incentivized compared to laboratory studies. I resolve a long-standing debate about whether professional players’ tennis serve directions are serially independent (Hsu, Huang & Tang, 2007) or not (Walker & Wooders, 2001) using a new dataset that is two orders of magnitude larger than those studies. I examine both between- and within-player determinants of the degree of serial (in)dependence. Evidence of the existence of significant serial dependence across serves is presented, even among players ranked Number 1 in the world. Furthermore, significant heterogeneity was found with respect to the strength of serial dependence and also its sign. A novel finding is that Number 1 and Number 2 ranked players tend to under-alternate on average, whereas in line with previous findings, the lower-ranked the players, the greater their tendency to over-alternate. Within-player analyses show that high-ranked players do not condition their randomization behavior on their opponent’s ranking. However, the under-alternation of top players would be consistent with a best-response to beliefs that the population of opponents over-alternates on average. Finally, the degree of observed serial dependence is not systematically related to other match variables proxying for match difficulty, fatigue, and psychological pressure.

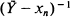 where
where 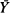 is the mean of the sample values overshooting
is the mean of the sample values overshooting 