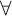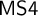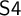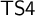Refine search
Actions for selected content:
1 results
TEMPORAL INTERPRETATION OF MONADIC INTUITIONISTIC QUANTIFIERS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 December 2021, pp. 164-187
- Print publication:
- March 2023
-
- Article
- Export citation