We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this note, we prove two monotonicity formulas for solutions of $\Delta _H f = c$
and $\Delta _H f - \partial _t f = c$
in Carnot groups. Such formulas involve the right-invariant carré du champ of a function and they are false for the left-invariant one. The main results, theorems 1.1 and 1.2, display a resemblance with two deep monotonicity formulas respectively due to Alt–Caffarelli–Friedman for the standard Laplacian, and to Caffarelli for the heat equation. In connection with this aspect we ask the question whether an ‘almost monotonicity’ formula be possible. In the last section, we discuss the failure of the nondecreasing monotonicity of an Almgren type functional.
In this paper, we discuss monotonicity formulae of various entropy functionals under various rescaled versions of Ricci flow. As an application, we prove that the lowest eigenvalue of a family of geometric operators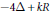 
$-4\Delta \,+\,kR$ is monotonic along the normalized Ricci flow for all 
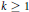$k\,\ge \,1$ provided the initial manifold has nonpositive total scalar curvature.
