Let 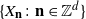 $\{X_{\textbf{n}} \colon \textbf{n}\in{\mathbb Z}^d\}$
be a weakly dependent stationary random field with maxima
$\{X_{\textbf{n}} \colon \textbf{n}\in{\mathbb Z}^d\}$
be a weakly dependent stationary random field with maxima 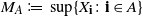 $M_{A} :=, \sup\{X_{\textbf{i}} \colon \textbf{i}\in A\}$
for finite
$M_{A} :=, \sup\{X_{\textbf{i}} \colon \textbf{i}\in A\}$
for finite 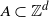 $A\subset{\mathbb Z}^d$
and
$A\subset{\mathbb Z}^d$
and 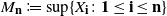 $M_{\textbf{n}} := \sup\{X_{\textbf{i}} \colon \mathbf{1} \leq \textbf{i} \leq \textbf{n} \}$
for
$M_{\textbf{n}} := \sup\{X_{\textbf{i}} \colon \mathbf{1} \leq \textbf{i} \leq \textbf{n} \}$
for  $\textbf{n}\in{\mathbb N}^d$
. In a general setting we prove that
$\textbf{n}\in{\mathbb N}^d$
. In a general setting we prove that 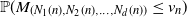 ${\mathbb{P}}(M_{(N_1(n),N_2(n),\ldots, N_d(n))} \leq v_n)$
${\mathbb{P}}(M_{(N_1(n),N_2(n),\ldots, N_d(n))} \leq v_n)$
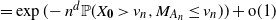 $= \exp(\!- n^d {\mathbb{P}}(X_{\mathbf{0}} > v_n , M_{A_n} \leq v_n)) + {\text{o}}(1)$
for some increasing sequence of sets
$= \exp(\!- n^d {\mathbb{P}}(X_{\mathbf{0}} > v_n , M_{A_n} \leq v_n)) + {\text{o}}(1)$
for some increasing sequence of sets 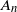 $A_n$
of size
$A_n$
of size 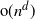 $ {\text{o}}(n^d)$
, where
$ {\text{o}}(n^d)$
, where 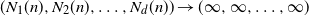 $(N_1(n),N_2(n), \ldots,N_d(n))\to(\infty,\infty, \ldots, \infty)$
and
$(N_1(n),N_2(n), \ldots,N_d(n))\to(\infty,\infty, \ldots, \infty)$
and 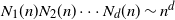 $N_1(n)N_2(n)\cdots N_d(n)\sim n^d$
. The sets
$N_1(n)N_2(n)\cdots N_d(n)\sim n^d$
. The sets 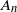 $A_n$
are determined by a translation-invariant total order
$A_n$
are determined by a translation-invariant total order 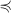 $\preccurlyeq$
on
$\preccurlyeq$
on 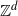 ${\mathbb Z}^d$
. For a class of fields satisfying a local mixing condition, including m-dependent ones, the main theorem holds with a constant finite A replacing
${\mathbb Z}^d$
. For a class of fields satisfying a local mixing condition, including m-dependent ones, the main theorem holds with a constant finite A replacing 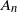 $A_n$
. The above results lead to new formulas for the extremal index for random fields. The new method for calculating limiting probabilities for maxima is compared with some known results and applied to the moving maximum field.
$A_n$
. The above results lead to new formulas for the extremal index for random fields. The new method for calculating limiting probabilities for maxima is compared with some known results and applied to the moving maximum field.