1 results
Symbolic Powers Versus Regular Powers of Ideals of General Points in ℙ1 × ℙ1
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 4 / 01 August 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 823-842
- Print publication:
- 01 August 2013
-
- Article
-
- You have access
- Export citation
-
Recent work of Ein–Lazarsfeld–Smith and Hochster–Huneke raised the problem of which symbolic powers of an ideal are contained in a given ordinary power of the ideal. Bocci–Harbourne developed methods to address this problem, which involve asymptotic numerical characters of symbolic powers of the ideals. Most of the work done up to now has been done for ideals defining 0-dimensional subschemes of projective space. Here we focus on certain subschemes given by a union of lines in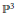
${{\mathbb{P}}^{3}}$ that can also be viewed as points in 
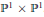${{\mathbb{P}}^{1}}\times {{\mathbb{P}}^{1}}$. We also obtain results on the closely related problem, studied by Hochster and by Li and Swanson, of determining situations for which each symbolic power of an ideal is an ordinary power.
