Let 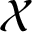 $\mathcal {X}$
be a Banach space over the complex field
$\mathcal {X}$
be a Banach space over the complex field 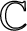 $\mathbb {C}$
and
$\mathbb {C}$
and 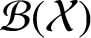 $\mathcal {B(X)}$
be the algebra of all bounded linear operators on
$\mathcal {B(X)}$
be the algebra of all bounded linear operators on 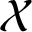 $\mathcal {X}$
. Let
$\mathcal {X}$
. Let  $\mathcal {N}$
be a nontrivial nest on
$\mathcal {N}$
be a nontrivial nest on 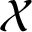 $\mathcal {X}$
,
$\mathcal {X}$
, 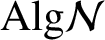 $\text {Alg}\mathcal {N}$
be the nest algebra associated with
$\text {Alg}\mathcal {N}$
be the nest algebra associated with  $\mathcal {N}$
, and
$\mathcal {N}$
, and 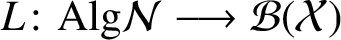 $L\colon \text {Alg}\mathcal {N}\longrightarrow \mathcal {B(X)}$
be a linear mapping. Suppose that
$L\colon \text {Alg}\mathcal {N}\longrightarrow \mathcal {B(X)}$
be a linear mapping. Suppose that 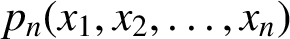 $p_n(x_1,x_2,\ldots ,x_n)$
is an
$p_n(x_1,x_2,\ldots ,x_n)$
is an 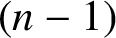 $(n-1)\,$
th commutator defined by n indeterminates
$(n-1)\,$
th commutator defined by n indeterminates 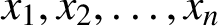 $x_1, x_2, \ldots , x_n$
. It is shown that L satisfies the rule
$x_1, x_2, \ldots , x_n$
. It is shown that L satisfies the rule 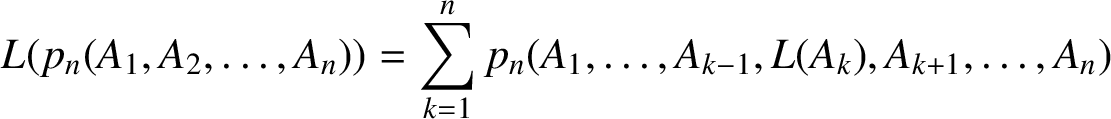 $$ \begin{align*}L(p_n(A_1, A_2, \ldots, A_n))=\sum_{k=1}^{n}p_n(A_1, \ldots, A_{k-1}, L(A_k), A_{k+1}, \ldots, A_n) \end{align*} $$
$$ \begin{align*}L(p_n(A_1, A_2, \ldots, A_n))=\sum_{k=1}^{n}p_n(A_1, \ldots, A_{k-1}, L(A_k), A_{k+1}, \ldots, A_n) \end{align*} $$
for all 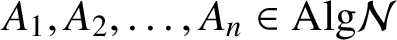 $A_1, A_2, \ldots , A_n\in \text {Alg}\mathcal {N}$
if and only if there exist a linear derivation
$A_1, A_2, \ldots , A_n\in \text {Alg}\mathcal {N}$
if and only if there exist a linear derivation 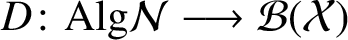 $D\colon \text {Alg}\mathcal {N}\longrightarrow \mathcal {B(X)}$
and a linear mapping
$D\colon \text {Alg}\mathcal {N}\longrightarrow \mathcal {B(X)}$
and a linear mapping 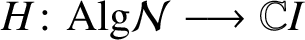 $H\colon \text {Alg}\mathcal {N}\longrightarrow \mathbb {C}I$
vanishing on each
$H\colon \text {Alg}\mathcal {N}\longrightarrow \mathbb {C}I$
vanishing on each  $(n-1)\,$
th commutator
$(n-1)\,$
th commutator 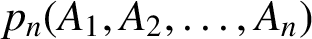 $p_n(A_1,A_2,\ldots , A_n)$
for all
$p_n(A_1,A_2,\ldots , A_n)$
for all 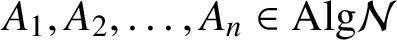 $A_1, A_2, \ldots , A_n\in \text {Alg}\mathcal {N}$
such that
$A_1, A_2, \ldots , A_n\in \text {Alg}\mathcal {N}$
such that 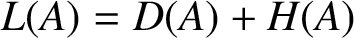 $L(A)=D(A)+H(A)$
for all
$L(A)=D(A)+H(A)$
for all 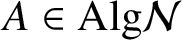 $A\in \text {Alg}\mathcal {N}$
. We also propose some related topics for future research.
$A\in \text {Alg}\mathcal {N}$
. We also propose some related topics for future research.