Let $v$ be a henselian valuation of any rank of a field $K$ and let 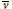$\bar{v}$ be the unique extension of $v$ to a fixed algebraic closure 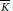$\overline{K}$ of $K$. In 2005, we studied properties of those pairs 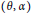$\left( \theta ,\,\alpha \right)$ of elements of 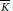$\overline{K}$ with 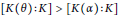$\left[ K\left( \theta \right):K \right]\,>\,\left[ K\left( \alpha \right):K \right]$ where $\alpha $ is an element of smallest degree over $K$ such that

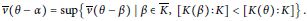$$\bar{v}\left( \theta \,-\,\alpha \right)\,=\,\sup \left\{ \bar{v}\left( \theta \,-\,\beta \right)\,|\,\beta \,\in \,\bar{K},\,\left[ K\left( \beta \right):K \right]\,<\,\left[ K\left( \theta \right):K \right] \right\}\,.$$

Such pairs are referred to as distinguished pairs. We use the concept of liftings of irreducible polynomials to give a different characterization of distinguished pairs.

Let $v$ be a Henselian Krull valuation of a field $K$. In this paper, the authors give some necessary and sufficient conditions for a finite simple extension of $(K,\,v)$ to be defectless. Various characterizations of algebraically maximal valued fields are also given which lead to a new proof of a result proved by Yu. L. Ershov.

Let $v$ be a henselian valuation of a field $K$ with value group $G$, let $\bar{v}$ be the (unique) extension of $v$ to a fixed algebraic closure $\bar{K}$ of $K$ and let $(\tilde{K},\tilde{v})$ be a completion of $(K,v)$. For $\alpha\in\bar{K}\setminus K$, let $M(\alpha,K)$ denote the set $\{\bar{v}(\alpha-\beta):\beta\in\bar{K},\ [K(\beta):K] \lt [K(\alpha):K]\}$. It is known that $M(\alpha,K)$ has an upper bound in $\bar{G}$ if and only if $[K(\alpha):K]=[\tilde{K}(\alpha):\tilde{K}]$, and that the supremum of $M(\alpha,K)$, which is denoted by $\delta_{K}(\alpha)$ (usually referred to as the main invariant of $\alpha$), satisfies a principle similar to the Krasner principle. Moreover, each complete discrete rank 1 valued field $(K,v)$ has the property that $\delta_{K}(\alpha)\in M(\alpha,K)$ for every $\alpha\in\bar{K}\setminus K$. In this paper the authors give a characterization of all those henselian valued fields $(K,v)$ which have the property mentioned above.

AMS 2000 Mathematics subject classification: Primary 12J10; 12J25; 13A18