We study the asymptotic behaviour as t → T–, near a finite blow-up time T > 0, of decreasing-in-x solutions to the following semilinear heat equation with a non-local term:
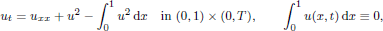
with Neumann boundary conditions and strictly decreasing initial function u0(x) with zero mass. We prove sharp estimates for u(x, t) as t → T–, revealing a non-uniform global blow-up:
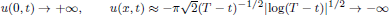
uniformly on any compact set [δ, 1], δ ∈ (0, 1).