In this paper, we establish the sharp asymptotic decay of positive solutions of the Yamabe type equation $\mathcal {L}_s u=u^{\frac {Q+2s}{Q-2s}}$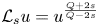 in a homogeneous Lie group, where $\mathcal {L}_s$
in a homogeneous Lie group, where $\mathcal {L}_s$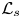 represents a suitable pseudodifferential operator modelled on a class of nonlocal operators arising in conformal CR geometry.
represents a suitable pseudodifferential operator modelled on a class of nonlocal operators arising in conformal CR geometry.