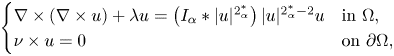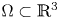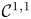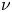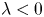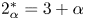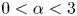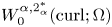1 results
On a critical time-harmonic Maxwell equation in nonlocal media
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 February 2024, pp. 1-45
-
- Article
-
- You have access
- HTML
- Export citation
-
In this paper, we study the existence of solutions for a critical time–harmonic Maxwell equation in nonlocal media
\[ \begin{cases} \nabla\times(\nabla\times u)+\lambda u=\left(I_{\alpha}\ast|u|^{2^{{\ast}}_{\alpha}}\right)|u|^{2^{{\ast}}_{\alpha}-2}u & \mathrm{in}\ \Omega,\\ \nu\times u=0 & \mathrm{on}\ \partial\Omega, \end{cases} \]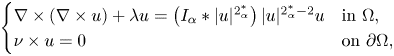where $\Omega \subset \mathbb {R}^{3}$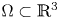
is a bounded domain, either convex or with $\mathcal {C}^{1,1}$
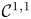boundary, $\nu$
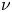is the exterior normal, $\lambda <0$
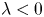is a real parameter, $2^{\ast }_{\alpha }=3+\alpha$
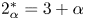with $0<\alpha <3$
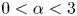is the upper critical exponent due to the Hardy–Littlewood–Sobolev inequality. By introducing some suitable Coulomb spaces involving curl operator $W^{\alpha,2^{\ast }_{\alpha }}_{0}(\mathrm {curl};\Omega )$
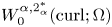, we are able to obtain the ground state solutions of the curl–curl equation via the method of constraining Nehari–Pankov manifold. Correspondingly, some sharp constants of the Sobolev-like inequalities with curl operator are obtained by a nonlocal version of the concentration–compactness principle.
