We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let 𝒳 be a space of homogeneous type in the sense of Coifman and Weiss. In this paper, two weighted estimates related to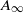 
weights are established for singular integral operators with nonsmooth kernels via a new sharp maximal operator associated with a generalized approximation to the identity. As applications, the weighted Lp(𝒳) and weighted endpoint estimates with general weights are obtained for singular integral operators with nonsmooth kernels, their commutators with BMO (𝒳) functions, and associated maximal operators. Some applications to holomorphic functional calculi of elliptic operators and Schrödinger operators are also presented.
