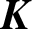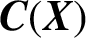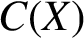This paper studies the work of Bak in algebra and (lower) algebraic K-theory and some later developments stimulated by them. We present an overview of his work in these areas, describe the setup and problems as well as the methods he introduced to attack these problems and state some of the crucial theorems. The aim is to analyse in detail some of his methods which are important and promising for further work in the subject. Among the topics covered are, unitary/general quadratic groups over form rings, structure theory and stability for such groups, quadratic K2 and the quadratic Steinberg groups, nonstable K-theory and localisation-completion, intermediate subgroups, congruence subgroup problem, dimension theory and surgery theory.
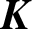 $\boldsymbol {K}$-STABILITY OF CONTINUOUS
$\boldsymbol {K}$-STABILITY OF CONTINUOUS 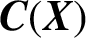 $\boldsymbol {C(X)}$-ALGEBRAS
$\boldsymbol {C(X)}$-ALGEBRAS