We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let 
where {λn}n ∈ Ζ is a sequence of real numbers such that |λn — n| ≤ Δ for some Δ > 0 and all n ∈ ℤ . Extending an obvious property of sin πz to which the function G reduces when Δ = 0 we show that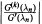 
is bounded by a constant independent of n. The result is then applied to a problem concerning derivative sampling in one and several variables.
