1 results
Avoiding families and Tukey functions on the nowhere-dense ideal
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 01 September 2010, pp. 405-435
- Print publication:
- April 2011
-
- Article
- Export citation
-
We investigate Tukey functions from the ideal of all closed nowhere-dense subsets of 2ℕ. In particular, we answer an old question of Isbell and Fremlin by showing that this ideal is not Tukey reducible to the ideal of density zero subsets of ℕ. We also prove non-existence of various special types of Tukey reductions from the nowhere-dense ideal to analytic P-ideals. In connection with these results, we study families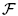
of clopen subsets of 2ℕ with the property that for each nowhere-dense subset of 2ℕ there is a set in 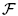not intersecting it. We call such families avoiding.
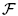of clopen subsets of 2