Search

In a planar smoothly bounded domain $\Omega$ , we consider the model for oncolytic virotherapy given by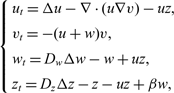

$$\left\{ \begin{array}{l} u_t = \Delta u - \nabla \cdot (u\nabla v) - uz, \\[1mm] v_t = - (u+w)v, \\[1mm] w_t = d_w \Delta w - w + uz, \\[1mm] z_t = d_z \Delta z - z - uz + \beta w, \end{array} \right.$$

with positive parameters

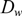$ D_w $ ,

$ D_z $ and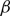

$\beta$ . It is firstly shown that whenever

$\beta \lt 1$ , for any choice of

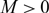$M \gt 0$ , one can find initial data such that the solution of an associated no-flux initial-boundary value problem, well known to exist globally actually for any choice of

$\beta \gt 0$ , satisfies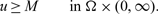

$$u\ge M \qquad \mbox{in } \Omega\times (0,\infty).$$

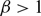$\beta \gt 1$ , however, then for arbitrary initial data the corresponding is seen to have the property that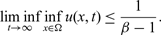

$$\liminf_{t\to\infty} \inf_{x\in\Omega} u(x,t)\le \frac{1}{\beta-1}.$$

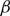This may be interpreted as indicating that

$\beta$ plays the role of a critical virus replication rate with regard to efficiency of the considered virotherapy, with corresponding threshold value given by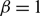

$\beta = 1$ .

Background:

Viral gene therapy is a promising new treatment modality for head and neck cancer. This paper provides the reader with a review of the relevant literature in this field.

Results:

There are government licensed viral gene therapy products currently in use for head and neck cancer, utilised in conjunction with established treatment modalities. The viruses target tumour-associated genes, with the first licensed virus replacing p53 gene function, which is frequently lost in tumourigenesis. Oncolytic viruses selectively destroy cancer cells through viral replication and can be armed with therapeutic transgenes.

Conclusion:

Despite considerable advances in this field over the last 40 years, further research is needed to improve the overall efficacy of the viruses and allow their widespread utilisation in the management of head and neck cancer.

Search Results

Refine search

Refine search

Actions for selected content:

3 results

A critical virus production rate for efficiency of oncolytic virotherapy

APPLICATIONS OF MATHEMATICAL MODELLING IN ONCOLYTIC VIROTHERAPY AND IMMUNOTHERAPY

Viral gene therapy for head and neck cancer

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

3 results

A critical virus production rate for efficiency of oncolytic virotherapy

APPLICATIONS OF MATHEMATICAL MODELLING IN ONCOLYTIC VIROTHERAPY AND IMMUNOTHERAPY

Viral gene therapy for head and neck cancer