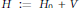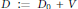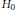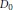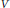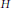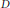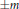Nous considérons les perturbations 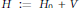 $H\,:=\,{{H}_{0}}\,+\,V$ et
$H\,:=\,{{H}_{0}}\,+\,V$ et 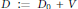 $D\,:=\,{{D}_{0}}\,+\,V$ des Hamiltoniens libres
$D\,:=\,{{D}_{0}}\,+\,V$ des Hamiltoniens libres 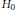 ${{H}_{0}}$ de Pauli et
${{H}_{0}}$ de Pauli et 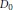 ${{D}_{0}}$ de Dirac en dimension 3 avec champ magnétique non constant,
${{D}_{0}}$ de Dirac en dimension 3 avec champ magnétique non constant, 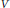 $V$ étant un potentiel électrique qui décroıt super-exponentiellement dans la direction du champ magnétique. Nous montrons que dans des espaces de Banach appropriés, les résolvantes de
$V$ étant un potentiel électrique qui décroıt super-exponentiellement dans la direction du champ magnétique. Nous montrons que dans des espaces de Banach appropriés, les résolvantes de 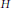 $H$ et
$H$ et 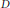 $D$ définies sur le demi-plan supérieur admettent des prolongements méromorphes. Nous définissons les résonances de
$D$ définies sur le demi-plan supérieur admettent des prolongements méromorphes. Nous définissons les résonances de 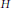 $H$ et
$H$ et 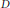 $D$ comme étant les pôles de ces extensions méromorphes. D’une part, nous étudions la répartition des résonances de
$D$ comme étant les pôles de ces extensions méromorphes. D’une part, nous étudions la répartition des résonances de 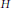 $H$ prés de l’origine 0 et d’autre part, celle des résonances de
$H$ prés de l’origine 0 et d’autre part, celle des résonances de 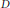 $D$ près de
$D$ près de 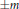 $\pm m$ où m est la masse d’une particule. Dans les deux cas, nous obtenons d’abord des majorations du nombre de résonances dans de petits domaines au voisinage de 0 et
$\pm m$ où m est la masse d’une particule. Dans les deux cas, nous obtenons d’abord des majorations du nombre de résonances dans de petits domaines au voisinage de 0 et 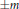 $\pm m$. Sous des hypothèses supplémentaires, nous obtenons des développements asymptotiques du nombre de résonances qui entraınent leur accumulation près des seuils 0 et
$\pm m$. Sous des hypothèses supplémentaires, nous obtenons des développements asymptotiques du nombre de résonances qui entraınent leur accumulation près des seuils 0 et 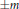 $\pm m$. En particulier, pour une perturbation
$\pm m$. En particulier, pour une perturbation 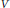 $V$ de signe défini, nous obtenons des informations sur la répartition des valeurs propres de
$V$ de signe défini, nous obtenons des informations sur la répartition des valeurs propres de 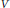 $H$ et
$H$ et 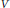 $D$ près de 0 et
$D$ près de 0 et 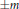 $\pm m$ respectivement.
$\pm m$ respectivement.