Classical definitions of weak higher-dimensional categories are given inductively, for example, a bicategory has a set of objects and hom categories, and a tricategory has a set of objects and hom bicategories. However, more recent definitions of weak n-categories for all natural numbers n, or of weak
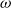 $\omega$
-categories, take more sophisticated approaches, and the nature of the ‘hom is often not immediate from the definitions’. In this paper, we focus on Leinster’s definition of weak
$\omega$
-categories, take more sophisticated approaches, and the nature of the ‘hom is often not immediate from the definitions’. In this paper, we focus on Leinster’s definition of weak
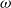 $\omega$
-category based on an earlier definition by Batanin and construct, for each weak
$\omega$
-category based on an earlier definition by Batanin and construct, for each weak
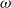 $\omega$
-category
$\omega$
-category
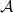 $\mathcal{A}$
, an underlying (weak
$\mathcal{A}$
, an underlying (weak
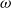 $\omega$
-category)-enriched graph consisting of the same objects and for each pair of objects x and y, a hom weak
$\omega$
-category)-enriched graph consisting of the same objects and for each pair of objects x and y, a hom weak
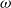 $\omega$
-category
$\omega$
-category
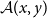 $\mathcal{A}(x,y)$
. We also show that our construction is functorial with respect to weak
$\mathcal{A}(x,y)$
. We also show that our construction is functorial with respect to weak
 $\omega$
-functors introduced by Garner.
$\omega$
-functors introduced by Garner.
