We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let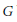 
$G$ be a locally compact group, and let 
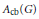${{A}_{\text{cb}}}(G)$ denote the closure of 
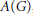$A(G)$, the Fourier algebra of 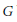$G$, in the space of completely bounded multipliers of 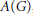$A(G)$. If 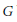$G$ is a weakly amenable, discrete group such that 
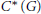${{C}^{*}}(G)$ is residually finite-dimensional, we show that 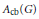${{A}_{\text{cb}}}(G)$ is operator amenable. In particular, 
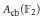${{A}_{\text{cb}}}({{\mathbb{F}}_{2}})$ is operator amenable even though 
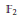${{\mathbb{F}}_{2}}$, the free group in two generators, is not an amenable group. Moreover, we show that if 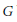$G$ is a discrete group such that 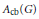${{A}_{\text{cb}}}(G)$ is operator amenable, a closed ideal of 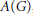$A(G)$ is weakly completely complemented in 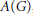$A(G)$ if and only if it has an approximate identity bounded in the 
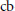$\text{cb}$-multiplier norm.
We prove a quantized version of a theorem by M. V. Sheĭnberg: A uniform algebra equipped with its canonical, i.e., minimal, operator space structure is operator amenable if and only if it is a commutative 
${{C}^{*}}$-algebra.
