When is an ideal of a ring radical or prime? By examining its generators, one may in many cases definably and uniformly test the ideal’s properties. We seek to establish such definable formulas in rings of p-adic power series, such as $\mathbb Q_{p}\langle X\rangle $ , $\mathbb Z_{p}\langle X\rangle $ , and related rings of power series over more general valuation rings and their fraction fields. We obtain a definable, uniform test for radicality, and, in the one-dimensional case, for primality. This builds upon the techniques stemming from the proof of the quantifier elimination results for the analytic theory of the p-adic integers by Denef and van den Dries, and the linear algebra methods of Hermann and Seidenberg.

Abstract prepared by Madeline G. Barnicle.

E-mail: barnicle@math.ucla.edu

URL: https://escholarship.org/uc/item/6t02q9s4

In [16], Peterzil and Steinhorn proved that if a group G definable in an o-minimal structure is not definably compact, then G contains a definable torsion-free subgroup of dimension 1. We prove here a p-adic analogue of the Peterzil–Steinhorn theorem, in the special case of abelian groups. Let G be an abelian group definable in a p-adically closed field M. If G is not definably compact then there is a definable subgroup H of dimension 1 which is not definably compact. In a future paper we will generalize this to non-abelian G.

The renormalization group method has been developed to investigate p-adic q-state Potts models on the Cayley tree of order k. This method is closely related to the examination of dynamical behavior of the p-adic Potts–Bethe mapping which depends on the parameters q, k. In Mukhamedov and Khakimov [Chaotic behavior of the p-adic Potts–Behte mapping. Discrete Contin. Dyn. Syst. 38 (2018), 231–245], we have considered the case when q is not divisible by p and, under some conditions, it was established that the mapping is conjugate to the full shift on $\kappa _p$ symbols (here $\kappa _p$ is the greatest common factor of k and $p-1$ ). The present paper is a continuation of the forementioned paper, but here we investigate the case when q is divisible by p and k is arbitrary. We are able to fully describe the dynamical behavior of the p-adic Potts–Bethe mapping by means of a Markov partition. Moreover, the existence of a Julia set is established, over which the mapping exhibits a chaotic behavior. We point out that a similar result is not known in the case of real numbers (with rigorous proofs).

In the 1993 Western Number Theory Conference, Richard Guy proposed Problem 93:31, which asks for integers n representable by 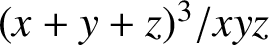${(x+y+z)^3}/{xyz}$ , where 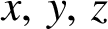$x,\,y,\,z$ are integers, preferably with positive integer solutions. We show that the representation 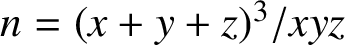$n={(x+y+z)^3}/{xyz}$ is impossible in positive integers 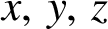$x,\,y,\,z$ if 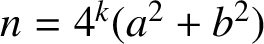$n=4^{k}(a^2+b^2)$ , where 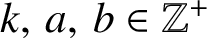$k,\,a,\,b\in \mathbb {Z}^{+}$ are such that 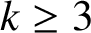$k\geq 3$ and 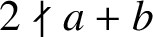$2\nmid a+b$ .

A complete list of one dimensional groups definable in the p-adic numbers is given, up to a finite index subgroup and a quotient by a finite subgroup.

This work focuses on the ongoing research of lineability (the search for large linear structures within certain non-linear sets) in non-Archimedean frameworks. Among several other results, we show that there exist large linear structures inside each of the following sets: (i) functions with a fixed closed subset of continuity, (ii) all continuous functions that are not Darboux continuous (or vice versa), (iii) all functions whose Dieudonné integral does not behave as an antiderivative, and (iv) functions with finite range and having antiderivative.

The quotient set of $A\subseteq \mathbb{N}$ is defined as $R(A):=\{a/b:a,b\in A,b\neq 0\}$. Using algebraic number theory in $\mathbb{Q}(\sqrt{5})$, Garcia and Luca [‘Quotients of Fibonacci numbers’, Amer. Math. Monthly, to appear] proved that the quotient set of Fibonacci numbers is dense in the $p$-adic numbers $\mathbb{Q}_{p}$ for all prime numbers $p$. For any integer $k\geq 2$, let $(F_{n}^{(k)})_{n\geq -(k-2)}$ be the sequence of $k$-generalised Fibonacci numbers, defined by the initial values $0,0,\ldots ,0,1$ ($k$ terms) and such that each successive term is the sum of the $k$ preceding terms. 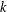We use $p$-adic analysis to generalise the result of Garcia and Luca, by proving that the quotient set of $k$-generalised Fibonacci numbers is dense in 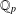$\mathbb{Q}_{p}$ for any integer $k\geq 2$ and any prime number $p$.

We show that the class of ${\cal L}$-constructible functions is closed under integration for any P-minimal expansion of a p-adic field $\left( {K,{\cal L}} \right)$. This generalizes results previously known for semi-algebraic and subanalytic structures. As part of the proof, we obtain a weak version of cell decomposition and function preparation for P-minimal structures, a result which is independent of the existence of Skolem functions. A direct corollary is that Denef’s results on the rationality of Poincaré series hold in any P-minimal expansion of a p-adic field $\left( {K,{\cal L}} \right)$.

We introduce a very weak language on p-adic fields K, which is just rich enough to have exactly the same definable subsets of the line K that one has using the ring language. (In our context, definable always means definable with parameters.) We prove that the only definable functions in the language are trivial functions. We also give a definitional expansion of in which K has quantifier elimination, and we obtain a cell decomposition result for -definable sets.

Our language can serve as a p-adic analogue of the very weak language (<) on the real numbers, to define a notion of minimality on the field of p-adic numbers and on related valued fields. These fields are not necessarily Henselian and may have positive characteristic.

Continuing earlier studies over the real numbers, we study the expressible set of a sequence A = (an)n≥1 of p-adic numbers, which we define to be the set EpA = {∑n≥1ancn: cn ∈ ℕ}. We show that in certain circumstances we can calculate the Haar measure of EpA exactly. It turns out that our results extend to sequences of matrices with p-adic entries, so this is the setting in which we work.

A ring in which every accessible subring is an ideal is called filial. We continue the study of commutative reduced filial rings started in [R. R. Andruszkiewicz and K. Pryszczepko, ‘A classification of commutative reduced filial rings’, Comm. Algebra to appear]. In particular we describe the Noetherian commutative reduced rings and construct nontrivial examples of commutative reduced filial rings without ideals which are domains.

We formulate and prove necessary and sufficient conditions for the Galois correspondence to hold for the ring of p-adic periods B+dR.