We compute the trivial source character tables (also called species tables of the trivial source ring) of the infinite family of finite groups 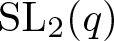 $\operatorname{SL}_{2}(q)$ for q even over a large enough field of odd characteristics. This article is a continuation of our article Trivial Source Character Tables of
$\operatorname{SL}_{2}(q)$ for q even over a large enough field of odd characteristics. This article is a continuation of our article Trivial Source Character Tables of 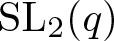 $\operatorname{SL}_{2}(q)$, where we considered, in particular, the case in which q is odd in non-defining characteristic.
$\operatorname{SL}_{2}(q)$, where we considered, in particular, the case in which q is odd in non-defining characteristic.
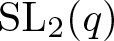 $\operatorname{SL}_2(q)$, part II
$\operatorname{SL}_2(q)$, part II