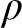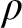1 results
WHAT IS A RULE OF INFERENCE?
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 21 December 2020, pp. 307-346
- Print publication:
- June 2021
-
- Article
- Export citation
-
We explore the problems that confront any attempt to explain or explicate exactly what a primitive logical rule of inference is, or consists in. We arrive at a proposed solution that places a surprisingly heavy load on the prospect of being able to understand and deal with specifications of rules that are essentially self-referring. That is, any rule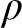
$\rho $
is to be understood via a specification that involves, embedded within it, reference to rule 
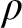$\rho $
itself. Just how we arrive at this position is explained by reference to familiar rules as well as less familiar ones with unusual features. An inquiry of this kind is surprisingly absent from the foundations of inferentialism—the view that meanings of expressions (especially logical ones) are to be characterized by the rules of inference that govern them.
