We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We give an example of a path-wise connected open set of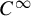 
$C^{\infty }$ partially hyperbolic endomorphisms on the 
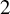$2$-torus, on which the (unique) Sinai–Ruelle–Bowen (SRB) measure exists for each system and varies smoothly depending on the system, while the sign of its central Lyapunov exponent changes.
