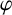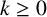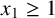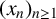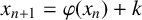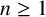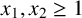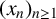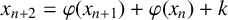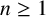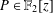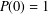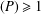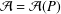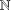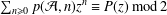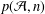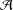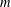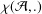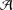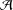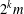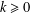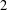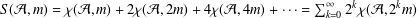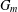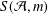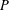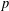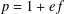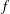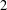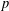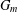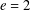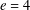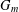Let 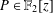$\varphi $ be Euler’s function and fix an integer $k\ge 0$. We show that for every initial value $x_1\ge 1$, the sequence of positive integers $(x_n)_{n\ge 1}$ defined by $x_{n+1}=\varphi (x_n)+k$ for all $n\ge 1$ is eventually periodic. Similarly, for all initial values $x_1,x_2\ge 1$, the sequence of positive integers $(x_n)_{n\ge 1}$ defined by $x_{n+2}=\varphi (x_{n+1})+\varphi (x_n)+k$ for all $n\ge 1$ is eventually periodic, provided that k is even.

Let $P\in \mathbb{F}_{2}[z]$ be such that 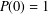$P(0)=1$ and degree 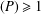$(P)\geq 1$. Nicolas et al. [‘On the parity of additive representation functions’, J. Number Theory73 (1998), 292–317] proved that there exists a unique subset 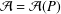${\mathcal{A}}={\mathcal{A}}(P)$ of 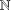$\mathbb{N}$ such that 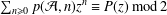$\sum _{n\geq 0}p({\mathcal{A}},n)z^{n}\equiv P(z)~\text{mod}\,2$, where 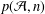$p({\mathcal{A}},n)$ is the number of partitions of $n$ with parts in 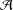${\mathcal{A}}$. Let 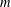$m$ be an odd positive integer and let 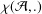${\it\chi}({\mathcal{A}},.)$ be the characteristic function of the set 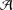${\mathcal{A}}$. Finding the elements of the set 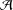${\mathcal{A}}$ of the form 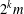$2^{k}m$, 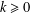$k\geq 0$, is closely related to the 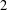$2$-adic integer 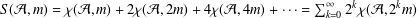$S({\mathcal{A}},m)={\it\chi}({\mathcal{A}},m)+2{\it\chi}({\mathcal{A}},2m)+4{\it\chi}({\mathcal{A}},4m)+\cdots =\sum _{k=0}^{\infty }2^{k}{\it\chi}({\mathcal{A}},2^{k}m)$, which has been shown to be an algebraic number. Let 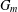$G_{m}$ be the minimal polynomial of 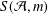$S({\mathcal{A}},m)$. In precedent works there were treated the case 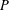$P$ irreducible of odd prime order 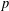$p$. In this setting, taking 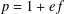$p=1+ef$, where 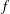$f$ is the order of 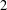$2$ modulo 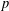$p$, explicit determinations of the coefficients of 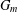$G_{m}$ have been made for 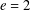$e=2$ and 3. In this paper, we treat the case 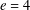$e=4$ and use the cyclotomic numbers to make explicit 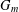$G_{m}$.