1 results
Stability Threshold for Scalar Linear Periodic Delay Differential Equations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 849-857
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation
-
We prove that for the linear scalar delay differential equation
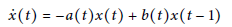$$\dot{x}\left( t \right)=-a\left( t \right)x\left( t \right)+b\left( t \right)x\left( t-1 \right)$$with non-negative periodic coefficients of period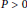
$p\,>\,0$, the stability threshold for the trivial solution is 
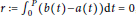$r\,:=\int_{0}^{p}{\left( b\left( t \right)-a\left( t \right) \right)}dt\,=\,0$, assuming that 
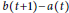$b\left( t+1 \right)-a\left( t \right)$ does not change its sign. By constructing a class of explicit examples, we show the counter-intuitive result that, in general, 
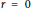$r\,=\,0$ is not a stability threshold.
