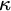 $\kappa $
-HOMOGENEOUS, BUT NOT
$\kappa $
-HOMOGENEOUS, BUT NOT
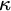 $\kappa $
-TRANSITIVE PERMUTATION GROUPS
$\kappa $
-TRANSITIVE PERMUTATION GROUPS