1 results
Generalized Solution of the Photon Transport Problem
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 1 / 01 March 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 28-38
- Print publication:
- 01 March 2011
-
- Article
-
- You have access
- Export citation
-
The purpose of this paper is to show the existence of a generalized solution of the photon transport problem. By means of the theory of equicontinuous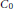
${{C}_{0}}$-semigroup on a sequentially complete locally convex topological vector space we show that the perturbed abstract Cauchy problem has a unique solution when the perturbation operator and the forcing term function satisfy certain conditions. A consequence of the abstract result is that it can be directly applied to obtain a generalized solution of the photon transport problem.
