We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We establish two results in the pointwise convergence problem of a trigonometric series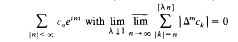 
for some nonnegative integer m. These results not only generalize Hardy's theorem, the Jordan test theorem and Fatou's theorem, but also complement the results on pointwise convergence of those Fourier series associated with known L1-convergence classes. A similar result is also established for the case that 
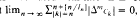, where {ln} satisfies certain conditions.
