For a polynomial progression

we define four notions of complexity: Host–Kra complexity, Weyl complexity, true complexity and algebraic complexity. The first two describe the smallest characteristic factor of the progression, the third refers to the smallest-degree Gowers norm controlling the progression, and the fourth concerns algebraic relations between terms of the progressions. We conjecture that these four notions are equivalent, which would give a purely algebraic criterion for determining the smallest Host–Kra factor or the smallest Gowers norm controlling a given progression. We prove this conjecture for all progressions whose terms only satisfy homogeneous algebraic relations and linear combinations thereof. This family of polynomial progressions includes, but is not limited to, arithmetic progressions, progressions with linearly independent polynomials $P_1, \ldots ,\!P_t$ and progressions whose terms satisfy no quadratic relations. For progressions that satisfy only linear relations, such as

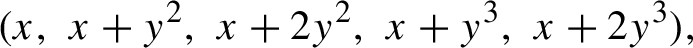$$ \begin{align*}(x,\; x+y^2,\; x+2y^2,\; x+y^3,\; x+2y^3),\end{align*} $$

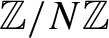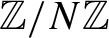we derive several combinatorial and dynamical corollaries: first, an estimate for the count of such progressions in subsets of $\mathbb {Z}/N\mathbb {Z}$ or totally ergodic dynamical systems; second, a lower bound for multiple recurrence; and third, a popular common difference result in $\mathbb {Z}/N\mathbb {Z}$ . Lastly, we show that Weyl complexity and algebraic complexity always agree, which gives a straightforward algebraic description of Weyl complexity.