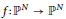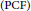The morphism $f\,:\,{{\mathbb{P}}^{N}}\,\to \,{{\mathbb{P}}^{N}}$ is called post-critically finite $\left( \text{PCF} \right)$ if the forward image of the critical locus, under iteration of 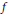$f$ , has algebraic support. In the case 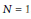$N\,=\,1$ , a result of Thurston implies that there are no algebraic families of PCF morphisms, other than a well-understood exceptional class known as the flexible Lattés maps. A related arithmetic result states that the set of PCF morphisms corresponds to a set of bounded height in the moduli space of univariate rational functions. 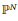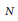We prove corresponding results for a certain subclass of the regular polynomial endomorphisms of ${{\mathbb{P}}^{N}}$ for any $N$ .