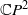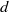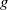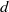Finding the so-called characteristic numbers of the complex projective plane $ \mathbb{C} {P}^{2} $ is a classical problem of enumerative geometry posed by Zeuthen more than a century ago. For a given $d$ and $g$ one has to find the number of degree $d$ genus $g$ curves that pass through a certain generic configuration of points and at the same time are tangent to a certain generic configuration of lines. The total number of points and lines in these two configurations is $3d- 1+ g$ so that the answer is a finite integer number. In this paper we translate this classical problem to the corresponding enumerative problem of tropical geometry in the case when $g= 0$. Namely, we show that the tropical problem is well posed and establish a special case of the correspondence theorem that ensures that the corresponding tropical and classical numbers coincide. Then we use the floor diagram calculus to reduce the problem to pure combinatorics. As a consequence, we express genus 0 characteristic numbers of $ \mathbb{C} {P}^{2} $ in terms of open Hurwitz numbers.

This is a contribution to the study of line-transitive groups of automorphisms of finite linear spaces. Groups which are almost simple are of particular importance. In this paper almost simple line-transitive groups whose socle is an alternating group are classified. It is proved that the only alternating groups to occur are those of degrees 7 and 8, and that only one linear space occurs, namely a well-known space with 15 points and 35 lines. Although much of the proof exploits special properties of alternating groups, some general theory of groups acting line-transitively on finite linear spaces is developed.