Two famous negative results about da Costa’s paraconsistent logic
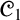 ${\mathscr {C}}_1$
(the failure of the Lindenbaum–Tarski process [44] and its non-algebraizability [39]) have placed
${\mathscr {C}}_1$
(the failure of the Lindenbaum–Tarski process [44] and its non-algebraizability [39]) have placed
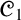 ${\mathscr {C}}_1$
seemingly as an exception to the scope of Abstract Algebraic Logic (AAL). In this paper we undertake a thorough AAL study of da Costa’s logic
${\mathscr {C}}_1$
seemingly as an exception to the scope of Abstract Algebraic Logic (AAL). In this paper we undertake a thorough AAL study of da Costa’s logic
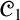 ${\mathscr {C}}_1$
. On the one hand, we strengthen the negative results about
${\mathscr {C}}_1$
. On the one hand, we strengthen the negative results about
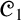 ${\mathscr {C}}_1$
by proving that it does not admit any algebraic semantics whatsoever in the sense of Blok and Pigozzi (a weaker notion than algebraizability also introduced in the monograph [6]). On the other hand,
${\mathscr {C}}_1$
by proving that it does not admit any algebraic semantics whatsoever in the sense of Blok and Pigozzi (a weaker notion than algebraizability also introduced in the monograph [6]). On the other hand,
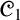 ${\mathscr {C}}_1$
is a protoalgebraic logic satisfying a Deduction-Detachment Theorem (DDT). We then extend our AAL study to some paraconsistent axiomatic extensions of
${\mathscr {C}}_1$
is a protoalgebraic logic satisfying a Deduction-Detachment Theorem (DDT). We then extend our AAL study to some paraconsistent axiomatic extensions of
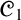 ${\mathscr {C}}_1$
covered in the literature. We prove that for extensions
${\mathscr {C}}_1$
covered in the literature. We prove that for extensions
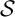 ${\mathcal {S}}$
such as
${\mathcal {S}}$
such as
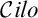 ${\mathcal {C}ilo}$
[26], every algebra in
${\mathcal {C}ilo}$
[26], every algebra in
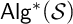 ${\mathsf {Alg}}^*({\mathcal {S}})$
contains a Boolean subalgebra, and for extensions
${\mathsf {Alg}}^*({\mathcal {S}})$
contains a Boolean subalgebra, and for extensions
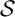 ${\mathcal {S}}$
such as
${\mathcal {S}}$
such as
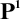 ,
,
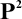 , or
, or
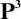 [16, 53], every subdirectly irreducible algebra in
[16, 53], every subdirectly irreducible algebra in
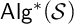 ${\mathsf {Alg}}^*({\mathcal {S}})$
has cardinality at most 3. We also characterize the quasivariety
${\mathsf {Alg}}^*({\mathcal {S}})$
has cardinality at most 3. We also characterize the quasivariety
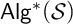 ${\mathsf {Alg}}^*({\mathcal {S}})$
and the intrinsic variety
${\mathsf {Alg}}^*({\mathcal {S}})$
and the intrinsic variety
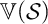 $\mathbb {V}({\mathcal {S}})$
, with
$\mathbb {V}({\mathcal {S}})$
, with
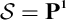 ,
,
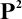 , and
, and
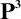 .
.
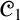 ${\mathscr {C}}_1$
AND SOME OF ITS PARACONSISTENT EXTENSIONS
${\mathscr {C}}_1$
AND SOME OF ITS PARACONSISTENT EXTENSIONS